Articulating a Pedagogy of Discussion
Re-Imagining Our Discussion Practice in Mathematics Methods
Introduction
Discussion, a core teaching practice (Grossman & Dean, 2019), focuses on student development of ideas. Research in mathematics education has focused on the use of discussion to teach mathematics (Smith & Stein, 2011; Walshaw & Anthony, 2008), with less attention to teacher educators’ discussion practice in the context of teaching about teaching (Loughran, 2006; Schuck & Brandenburg, 2020). However, practices used to discuss mathematical ideas do not necessarily transfer to discussions of pedagogical ideas (Steele, 2005) where sociopedagogical norms (Dick et al., 2018) may differ from sociomathematical norms (Yackel & Cobb, 1996). Calls for research on development of teacher educators’ practices (Krainer et al., 2021; Schuck & Brandenburg, 2020; Vanassche & Berry, 2020) motivated our desire to understand teacher educators’ development of discussion practices. As mathematics teacher educators (MTEs) focused on the pedagogical preparation of mathematics teachers, we uncover our pedagogy of discussion through exploration of our own discussion practices in mathematics methods courses. We unpack research that revealed our pedagogy of discussion about teaching with prospective teachers (PTs), allowing us to identify areas for growth in our discussion practices and articulate a pedagogy for discussion practice useful to the broader MTE community.
Context
We are white critical friends (Schuck & Russell, 2005) from three different U. S. universities who draw from constructivist teaching epistemology (Steffe & D’Ambrosio, 1995). We apply a perspective of relational teacher education (Kitchen, 2005) in mathematics methods courses as we collaboratively examine our practices to improve them and contribute to literature on mathematics teacher educator practice. Authors of this paper teach mathematics methods with this common theoretical perspective yet are situated in different institutional contexts. Signe teaches in an elementary teacher certification program at a research-intensive university, Alyson teaches secondary PTs at a research-focused university, and Susan teaches elementary PTs at a teaching-focused university.
The authors draw from constructivist epistemology in their pedagogy (Steffe & D’Ambrosio, 1995) of teaching about teaching. Our common view of learning about teaching includes creating and using models of PTs’ knowledge of mathematics teaching to inform our instructional decisions, such as the development of discussion questions. We position PTs as corroborators for knowledge about mathematics teaching and its development. Our reliance on PTs requires that we build models of our practice and identify any “living contradictions” (Whitehead, 1989, p. 41) between our pedagogy and evidence of our practice. Although our institutional contexts vary, we each gathered and collaboratively analyzed our data to become conscious of our pedagogy of discussion practice in mathematics methods courses.
Our teaching practices are undergirded by a relational teacher education perspective (Kitchen, 2005) which implies we take up PTs’ ideas and experiences and are receptive “to growing in relation” (Kitchen, 2005, p. 18) with our PTs. Regarding pedagogy of discussion, our perspective means we create space to learn about and use models of PTs’ thinking to plan discussions that support their understanding of the significance of discussion topics (Dillon, 1994) as related to their own teaching practices.
Following Loughran (2006), we recognize pedagogy as a theory of teaching and learning that results in knowledge growth through practice. Teacher education pedagogy maintains a complementary connection between teaching about teaching and learning about teaching (Loughran, 2014). According to Loughran, modeling of practices is an important component of pedagogy, but also requires that decisions involved in such practices be communicated. Development and analysis of MTE’s pedagogy begins with practices they use to teach about teaching. Grossman et al. (2009) cautioned that instructors’ “planning, modeling, and feedback” (p. 2090) mediate “learning potential” (p. 2089) of professional practice, raising questions about how MTE’s pedagogies inform practices. We focus on MTEs’ pedagogy of discussion practice with the question: What is our pedagogy of discussion practice in mathematics methods?
Discussion is defined as human interaction to address “a question of common concern” (Dillon, 1994, p. 8) through an exchange of ideas (Alexander, 2019) and an examination of differing viewpoints (Kim & Wilkinson, 2019). We differentiate discussion from recitation, in that interactions in the two forms of talk are distinct from the point of view of observers, and note that our interest is in developing discussions as opposed to recitations. In discussions, participants explore differing views of the common concern “to form their answer” (Dillon, 1994, p. 8). The result of such discussions is enhanced knowledge, understanding, appreciation, and judgements that inform actions. Recitation instead focuses on questions of concern to the issues at stake, but perhaps not of common concern to those addressing the question. We define discussion as a talk strategy MTEs use to support PTs’ development of knowledge and perspectives of concepts relevant to mathematics teaching practice. Teacher educators’ use of discussion practice is informed by their efforts to develop “knowledge from practice” (Pinnegar & Hamilton, 2009, p. 17) as a way of “knowing to” (p. 18) engage PTs in discussion. Discussion is used by MTEs to support PTs’ development of teaching, yet research points to the difficulty of enacting discussions that embody our definition (e.g., Reynolds, 2016). We have investigated the role of questions in building discussions, creating imbalance in practice, and in initiating discussion (Kastberg et al., 2019, 2020), resulting in identification of characteristics necessary but not sufficient for discussions to occur. These results suggested that our discussion practice was guided by more than questions, and thus initiated our investigation into our pedagogy of discussion practice.
Further informing exploration of our pedagogy of discussion, is the context within mathematics and phenomenological factors (e.g., social groups’ ways of operating; Dillon, 1994) that influence discussions. MTEs’ practices draw from PTs’ mathematics experiences and MTEs’ teaching of mathematics. PTs’ mathematics learning experiences inform their practices (Drake, 2006; Mewborn, 1999; Mewborn & Tyminski, 2006; Towers et al., 2017). MTEs assume PTs’ experiences shape responses to discussion questions. MTEs’ experiences facilitating mathematics discussions inform tacit knowledge of productive discussions (Munby & Russell, 1994) in mathematics education. Yet Steele’s (2005) finding that mathematics teachers draw from values and experience to support pedagogical claims suggests that MTEs’ experience facilitating mathematics discussions is of limited use in facilitating pedagogical discussions. The search for pedagogy of discussion in the teaching of teaching mathematics could not rely solely on our experiences as facilitators of discussions of mathematics. Phenomenological factors (Dillon 1994) inform MTEs’ facilitation of pedagogical discussions (Kastberg et al., 2020, 2021). PTs’ sense of community and relevant common experiences ground pedagogical discussions. MTEs’ facilitation of discussions, including structuring discussion questions, supporting interpretation of the question, and constraining evidence PTs use to address the question, impacts the form (i.e., IRE, recitation, discussion) and content of PTs’ talk (Lischka et al., 2021).
Pinnegar and Hamilton (2009) asserted “knowledge, theories, and understandings” (p. 16) inform teacher educator practices. One theory relevant to planning for and facilitating discussions is whole-class scaffolding. Whole-class scaffolding is used to support students’ concept development. Bakker et al. (2015) asserted whole-class scaffolding can ground instructor practice. Smit et al. (2013) described whole-class scaffolding as involving diagnosing and responding to student understandings and needs, while fostering independence (Visnovska & Cobb, 2015). Whole-class scaffolding is “layered, distributed and cumulative” (Smit et al., 2013, p. 829) and takes place before, during, and after whole-class interactions. Through this study, we developed consciousness of characteristics of whole-class scaffolding (Bakker et al., 2015; Smit et al., 2013; Visnovska & Cobb, 2015) which revealed our pedagogy of discussion practice as interpreting PTs’ understanding, responding to current understanding, and supporting movement toward independence in PTs’ teaching practice.
Aim
Our perspective on pedagogy requires maintenance of the connection between teaching about teaching and learning about teaching (Loughran, 2014). Although our prior research identified characteristics of discussion practice (Kastberg et al., 2019, 2020), we lacked articulation of the underlying pedagogy where teaching and learning are connected through that discussion practice. Whereas we seek more than “fixing” our practice (Vanassche & Berry, 2020, p. 207), we strive to become conscious of our pedagogy of discussion practice and therefore aimed to address the question: What is our pedagogy of discussion practice in mathematics methods? We seek to understand connections between teaching about teaching and learning about teaching (Loughran, 2014) so that we might better enact practice that maintains this connection. Using in-time and retrospective investigation of our practices, we build understanding of our pedagogy to inform our future work and provide a vehicle for engaging others in developing their practice of discussions of teaching.
Methods
Self-study methodology, a form of practitioner research (Borko et al., 2007), supports inquiry into pedagogy of practice. Self-study is self-initiated, improvement-aimed, interactive, uses qualitative methods, and defines validity as based in trustworthiness (LaBoskey, 2004). In this work, we “conceptualiz[e] what is actually happening in practice” (Vanassche & Berry, 2020, p. 188) as we enact our pedagogy of discussion, recognizing that our pedagogy is “constantly evolving and developing from experience” (p. 188).
We are three female MTEs who have engaged in self-study since 2013. We collaborate as critical friends to interrogate our pedagogy of discussion practice. Each of us taught mathematics before becoming MTEs and during this study we all taught mathematics methods courses. At our respective U.S. institutions, we have autonomy to improve our practice as we find appropriate. Structures that support research into one’s teaching differ at each institution. For example, institutional expectations related to faculty engagement in research and teaching responsibilities vary. Class sizes in each of our courses make engaging in whole-class discussions possible, yet we acknowledge that social structures developed in each program that support discussion vary (Dillon, 1994). For example, Alyson’s institution supports PTs’ to develop community across courses by engaging PTs in informal events while Susan and Signe’s institutions do not.
Susan had 26 years of experience as a MTE, teaching primarily elementary mathematics methods courses to PTs who are majority white female and commute from rural areas to the small (enrollment < 9000) midwestern teaching-focused state university. Susan’s discussion topic for this study was: How does cognitive demand of tasks and knowledge of children’s mathematical thinking inform planning instruction? Signe had 20 years of experience as a MTE, most recently teaching elementary mathematics methods courses at a large (enrollment >40,000) midwestern research-intensive university to PTs who are primarily white females from a variety of rural and urban backgrounds. Signe’s study of discussion practice focused on PTs’ views of learners’ mathematics guided by the question: How do children learn mathematics? Alyson had 12 years of experience as a MTE, teaching secondary mathematics methods within a teacher certification program at a large (enrollment > 22,000) southeastern state research-focused university where PTs are majority white with a variety of rural and urban backgrounds and take courses as a cohort with structures to purposefully create a learning community. Alyson’s program was intentionally increasing attention on issues of equity and diversity. In alignment with this initiative, her discussion for this study was guided by the question: What is the role of mathematics teachers related to social justice and equity?
Our institutional contexts and teaching responsibilities vary, yet we draw from a common theoretical perspective and desire to improve our feedback, questioning, and discussion practices. Although we view our teacher education practice holistically, exploration of each practice led to new questions about related practices. The exploration of our feedback practice (Kastberg et al., 2018) led to interrogating our questioning practices (Kastberg et al., 2019, 2020) that evolved into studying the pedagogy of our discussion practices (Kastberg et al, 2021).
Within self-study methodology, we used three qualitative analytic methods: analytical dialogues (Guilfoyle et al., 2004), evidentiary maps (Jordan & Henderson, 1995), and descriptive coding (Saldana, 2016). Evidence of pedagogy of discussion practice includes our experiences and associated artifacts of teaching gathered during August-December 2020. Our data is drawn from a variety of sources including transcripts of weekly critical friend conversations (analytical dialogues; Guilfoyle et al., 2004) and artifacts from our teaching (e.g., interactive slides, transcripts of class discussions, submitted work from PTs). Data was analyzed in three ways: (1) dialogic analysis of events in our discussion practice during seven August-December 2020 critical friend meetings leading to themes informing our practice; (2) creation and analysis of evidentiary maps (Jordan & Henderson, 1995) that captured the temporal nature of our discussion practice and revealed supporting or contradictory evidence for themes from the dialogic analysis; and (3) descriptive coding (Saldana, 2016) of transcripts using themes identified during the dialogic analysis while looking for evidence of other themes. Weekly analytical dialogues (Guilfoyle et al., 2004) about facilitating discussions in mathematics methods supported awareness of our discussion practice and perspective taking as we questioned working models of our practice. Pinnegar and Hamilton (2009) have described dialogues in communities as a mechanism of “coming to know” (p. 81) that affords practitioners with opportunities to gain perspective on their practice. During August-December 2020 our analytical dialogues of discussion practice supported coming to know that served as the basis for “action” (Guilfoyle et al., 2004, p. 1111) in our ongoing discussion practices. Ideas shared during dialogues were unpacked, analyzed, and critiqued resulting in the identification of two recurring themes in our planning for and implementation of discussion practice.
In January-May 2021 we created evidentiary maps of the “structure of events” (Jordan & Henderson, 1995, p, 57) in our discussion practice from course artifacts. Trustworthiness is addressed through the use of course artifacts from teaching and the insights we gained into our discussion practice that demonstrate emerging ideas and knowledge (Grant & Lincoln, 2021). Evidence confirming or contradicting initial findings from the dialogic analysis was identified.
Descriptive coding (Saldana, 2016) of transcripts from the August-December 2020 analytical dialogues was used to triangulate results from analytic dialogues and evidentiary maps. By combining data from in-time examination of our practice (i.e., the analytical dialogues that took place as we enacted our discussion practice) with retrospective analysis of those dialogues alongside evidentiary maps we developed an image of our pedagogy of discussion. Although our institutional contexts, past experiences as mathematics teachers and MTEs, and teaching responsibilities vary, analysis revealed evidence of commonalities across our pedagogies of discussion practice. Though there are unique elements in our discussion practices, the congruences illustrated a common pedagogy of discussion practice.
Outcomes
Our pedagogy of discussion is supported by two processes of whole-class scaffolding: anticipating and layering (Smit et al., 2013) as depicted in Figure 1. We consider anticipating a two-step action of gathering information about PTs’ knowledge, experiences, and feelings and using this evidence to predict ways PTs might respond in discussion. Anticipating informs MTEs’ planned interactions with PTs and spontaneous talk moves as MTEs engage with PTs during class. Layering occurs when instructors use anticipating in conjunction with the design of instructional activities. Instructional activities provide multiple opportunities to anticipate PTs’ thinking, with each occurrence adding more information to MTEs’ knowledge to inform discussion facilitation, as if creating a spiral moving toward the goal of independence in PTs’ teaching practice. In Figure 1, anticipating is depicted in the rectangles, solid and dashed arrows, and the blue enactment bubbles, as anticipating is an act that is not limited by time or space. Layering is depicted by the darkening of the bubbles from left to right, as additional activities produce more evidence of PTs’ thoughts and feelings for the MTE. Although analysis of each authors’ data contributed to findings, we demonstrate the emergence of our understanding of these whole-class scaffolding processes using excerpts from our critical friend conversations and descriptions of Alyson’s discussion practice.
Figure 1
A Model of Our Pedagogy of Discussion Practice in Mathematics Methods
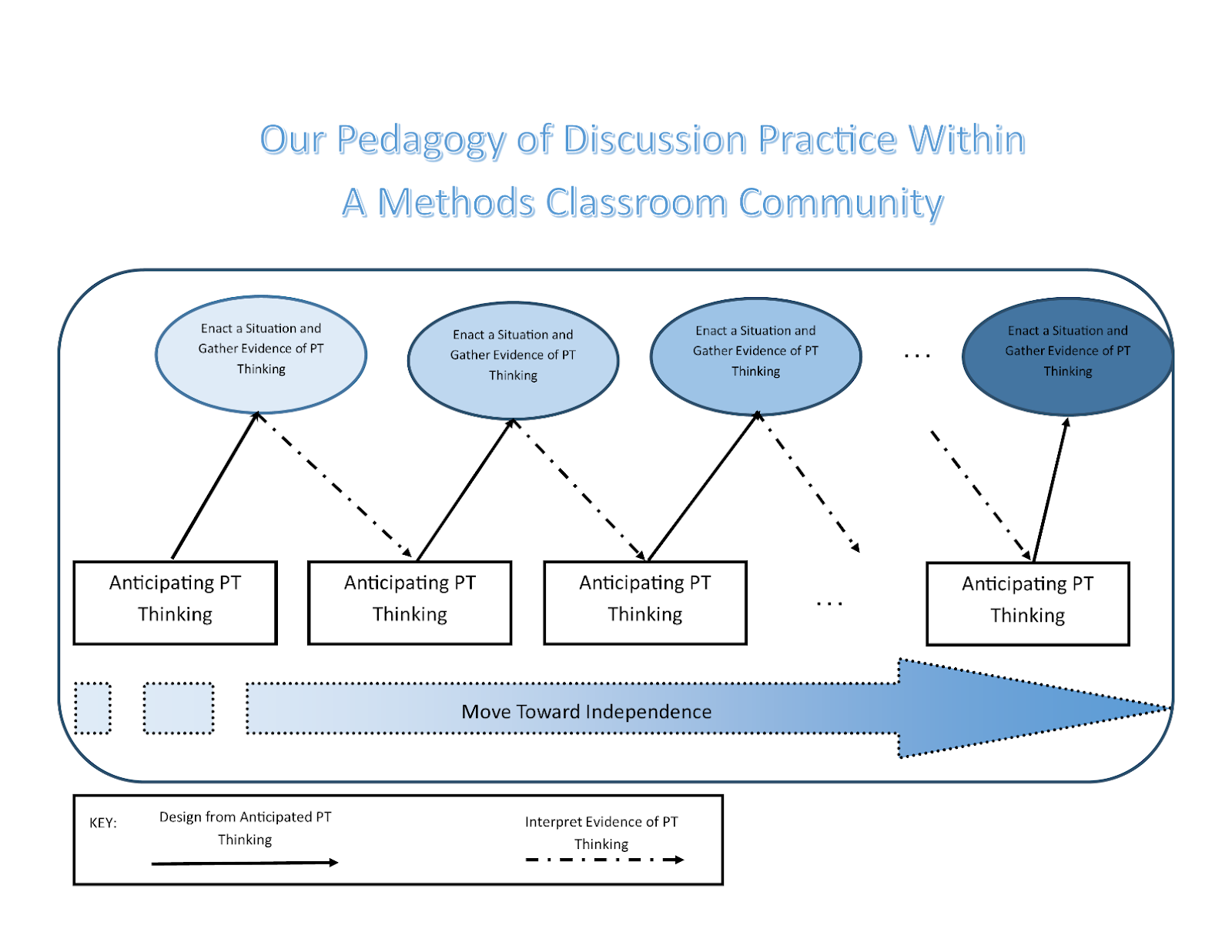
In Summer 2020 Alyson planned to facilitate discussions of social justice and equity in teaching secondary mathematics with PTs, a theme elevated in prominence in her August-December 2020 methods course due to program initiatives at her institution. In critical friend meetings during August-December 2020, we helped each other negotiate changes due to Covid-19 while keeping focus on goals around discussions of teaching in methods. We each described plans for discussions for August-December 2020, where Signe focused on discussion around what constitutes learning and Susan focused on ideas about cognitive demand.
Alyson planned a sequence of instructional activities related to equity and social justice including surveys of dispositions, readings and related discussion boards, and rehearsals of social justice lessons. As we returned to Dillon’s phenomenological characteristics for discussion communities (see Kastberg et al., 2019), new questions arose for us. Susan reacted to one of our early turns toward anticipating as we discussed the difficulties of gathering information to use when facilitating discussions at the moment:
This has me thinking back to Signe, when you came to see my lesson, and you were asking me these questions like, what do you anticipate? And how's it going to go? And I don't know. I honestly don't know, and I felt really stuck. (Critical Conversation, 8/31/20).
This dialogue helped Alyson realize how she could draw information from PTs’ experiences and then better leverage that information in discussions:
I need to go read those [PTs’ posts] and really think about what are the different things that they're saying? And how do I think about what's good about what they're saying, and what's bad about what they're saying? So that I have ways to draw on that conversation. (Critical Conversation, 08/31/20)
Alyson could use PTs’ individual assignments to anticipate contributions PTs might offer and plan how to facilitate discussion with PTs’ ideas in mind. Later in the same conversation, Alyson pushed us to consider how evidence to inform anticipation can be collected by intentionally designing layers of activities:
So what are some of the exit tickets or short, reflective responses that you might ask your students to turn in to you and help you with that anticipating process? Because I think before we've just said, ‘Well, I don't know what they're going to come up with!’ (Critical Conversation, 08/31/20)
Following this conversation, each author inserted additional instructional activities to gather evidence to support our anticipation of PTs’ thinking as we planned for discussions. Alyson included additional exit ticket questions for her PTs such as “What do you wonder about “school mathematics” after reading the Spencer and Hand chapter?” (Day 6 Exit Question) and “Thinking back over all of our equity readings so far, what do you notice? What do you wonder? What do you think about mathematics teachers’ roles in equity?” (Day 14 Exit Question). Similarly, Signe inserted questions to gauge insights about learning: “Finish the sentence: Conceptual knowledge for subtracting is different from procedural knowledge because….” Susan selected examples from PTs’ responses to use in subsequent class sessions.
Throughout August-December 2020 our ideas about the iterative and unbounded nature of planning for and facilitating discussions of teaching developed. Alyson’s ideas generated a critical friend conversation about the temporal boundaries of a pedagogical discussion. Alyson, while puzzling about where learning resides in a discussion, drew from her constructivist epistemology. Alyson reflected on dissonance as a trigger for PTs’ opportunities to learn.
I think I've been so focused on where the learning is in the discussion, that I haven't been paying attention to other things that are causing them to hit a point of dissonance in their understanding? (Critical Conversation, 11/10/2020)
We identified the unbounded nature of discussions of teaching that do not happen in a single class but instead evolve across layers of activities that produce opportunities for learning through discussion.
Alyson: We had a picture in our heads of something [a discussion] that would happen within a class period. And I think we're shifting that and now say it's not quite where it is. Think about the feedback discussion that my students have. That's something that goes on all semester long, it gets visited at different points.
...
Signe: So, you know, this, going iteratively, the way that we did over the course of the semester, shows me that PTs' seemingly divergent points of view, actually are convergent, with many PTs talking about it [learning]. (Critical Conversation, 11/10/2020)
Critical friend conversations continued into January-May 2021 after the in-class August-December 2020 data collection ended. Early in January we mapped out instructional activities related to each discussion topic and brought those to our meetings for further discussion. These maps, later termed evidentiary maps (Jordan & Henderson, 1995), provided focus for reflective conversations that continued in January-May 2021. Retrospective examination of August-December 2020 conversation transcripts alongside evidentiary maps revealed that anticipating PTs’ thinking and experiences and layering activities allowed MTEs to further anticipate PTs’ thinking. These processes were central in our pedagogy of discussion practice in mathematics methods.
Discussion
We employed collaborative self-study to move beyond identifying characteristics of our discussion practice to address the question: What is our pedagogy of discussion practice? Grossman et al. (2009) identified practices teacher educators use to inform opportunities PTs have for learning. Our outcomes illustrate how scaffolding whole-class discussions as a pedagogy of discussion practice informs such decisions. Across class sessions and outside of class, MTEs use PTs’ responses to make sense of PTs’ thinking. Additional evidence of PTs’ thinking allows MTEs to further anticipate PTs’ responses to new instructional activities. Layering and anticipating are two processes we tacitly used to plan for and facilitate whole class discussions. Class discussions involve whole-class scaffolding, a pedagogy made up of a collection of thoughts and actions (Smit et al., 2013). Typically scaffolding is described as actions that support learning, but the work of Bakker et al. (2015) identified whole-class scaffolding as informing teacher pedagogy and including layering activities, analysis, and response to student understanding. Because scaffolding involves maintaining a connection between MTEs’ actions of teaching about teaching and evidence of PTs’ learning about teaching, we claim that the processes we identified in our discussion practice are part of whole-class scaffolding as a pedagogy of discussion practice. Further, this element of our pedagogy points to the ways in which we can maintain a connection between teaching and learning about teaching.
By conducting this research through in-time and retrospective investigation, we acknowledge that MTE “knowledge is not a fixed state that can be achieved, but something that constantly develops from and through experience, and that is enacted – and only becomes “real” or “visible” – in practice” (Vanassche & Berry, 2020, p. 188). Articulating our pedagogy of discussion practice allows us to continue to develop that pedagogy and practices within it in more deliberate ways. Dialogue with co-authors supported Alyson to reassess the timing of whole-class discussions. Discussions were shifted to later in the course after PTs had developed shared experiences with social justice and equity and had understandings of the significance of social justice and equity for mathematics teaching. Anticipating PTs’ experiences informed layering of instructional activities relevant to discussion of teaching, with each layer providing new opportunities for MTE’s anticipating and support for PTs’ independent teaching practices.
Consciousness of our pedagogy of discussion practice allows us to describe discussion practice and move beyond providing models of discussion practice (Loughran, 2014). We focus on PTs’ understanding of terminology used in discussion questions and the significance of such questions for their teaching. In discussions of mathematics, we attended primarily to terms used in our questions and prior knowledge as we planned instructional activities. In planning for discussions of teaching, we attended to terminology, but also to the relevance of our discussion questions to teachers’ evolving views of teaching and the significance of discussion questions to those views. Although anticipating responses is a prominent practice in the teaching of mathematics concepts (Smith & Stein, 2011), we found that anticipation takes a different form when teaching about teaching. For our goal of engaging in discussions of teaching, anticipating requires the layering of multiple activities that allow anticipating to occur over time, so that we understand better the experiences and beliefs PTs might draw on in discussions of teaching. This extension of Steele’s (2005) finding points to the nuanced differences between discussions for learning mathematical content and discussions for learning about teaching mathematics. The knowledge gained through anticipation included a wider variety of aspects of PTs’ knowledge. Through this articulation, we address calls for research into teacher educator practice (Krainer et al., 2021) and Reynolds’ (2016) query regarding nuances in teacher-student discussion exchanges that support PTs’ practices.
References
Alexander, R. (2019). Whose discourse? Dialogic pedagogy for a post-truth world. Dialogic Pedagogy: An International Online Journal, 7. https://doi.org/10.5195/dpj.2019.268
Bakker, A., Smit, J., & Wegerif, R. (2015). Scaffolding and dialogic teaching in mathematics education: Introduction and review. ZDM, 47(7), 1047–1065. https://doi.org/10.1007/s11858-015-0738-8
Borko, H., Liston, D., & Whitcomb, J. (2007). Genres of empirical research in teacher education. Journal of Teacher Education, 58(1), 3–11. https://doi.org/10.1177/0022487106296220
Dick, L. K., Sztajn, P., White, T. F., & Heck, D. J. (2018). Investigating sociopedagogical norms: Teachers' discussions about own and others' instruction. Teaching and Teacher Education, 71, 297–307. https://doi.org/10.1016/j.tate.2018.01.004
Dillon, J. T. (1994). Using discussions in classrooms. Open University Press.
Drake, C. (2006). Turning points: Using teachers’ mathematics life stories to understand the implementation of mathematics education reform. Journal of Mathematics Teacher Education, 9(6), 579–608. https://doi.org/10.1007/s10857-006-9021-9
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., & Williamson, P. W. (2009). Teaching practice: A cross-professional perspective. Teachers College Record, 111(9), 2055–2100. https://doi.org/10.1177/016146810911100905
Grossman, P., & Dean, C. G. P. (2019). Negotiating a common language and shared understanding about core practices: The case of discussion. Teaching and Teacher Education, 80, 157–166. https://doi.org/10.1016/j.tate.2019.01.009
Guilfoyle, K., Hamilton, M. L., Pinnegar, S., & Placier, P. (2004). The epistemological dimensions and dynamics of professional dialogue in self-study. In J. J. Loughran, M. L. Hamilton, V. K. LaBoskey, & T. Russell (Eds.) International Handbook of Self-Study of Teaching and Teacher Education Practices (pp. 1109–1168). Springer. https://doi.org/10.1007/978-1-4020-6545-3_28
Grant, M. R., & Lincoln, Y. (2021). A conversation about rethinking criteria for qualitative and interpretive research: Quality as trustworthiness. Journal of Urban Mathematics Education, 14(2), 1–15. https://journals.tdl.org/jume
Jordan, B., & Henderson, A. (1995). Interaction analysis: Foundations and practice. The Journal of the Learning Sciences, 4(1), 39–103. https://doi.org/10.1207/s15327809jls0401_2
Kastberg, S., Lischka, A. E., & Hillman, S. (2018). Characterizing mathematics teacher educators’ written feedback to prospective teachers. Journal of Mathematics Teacher Education, 23(2), 131–152. https://doi.org/10.1007/s10857-018-9414-6
Kastberg, S. E., Lischka, A. E., & Hillman, S. L. (2019). Exploring mathematics teacher educator questioning as a relational practice: Acknowledging imbalances. Studying Teacher Education: A Journal of Self-Study of Teacher Education Practices, 15(1), 67–81. https://doi.org/10.1080/17425964.2018.1541278
Kastberg, S. E., Lischka. A. E., & Hillman, S. L. (2020). Weaving discussions with questioning. In C. Edge, A. Standerford, & B. Bergh (Eds.), Textiles and Tapestries: Self-Study for Envisioning New Ways of Knowing (pp 623–632). EdTech Books. https://edtechbooks.org/textiles_tapestries_self_study/weaving_discussions_.
Kastberg, S. E., Lischka, A. E., & Hillman, S. L. (2021). Revealing the pedagogy of discussion in mathematics methods. In D. Olanoff, K. Johnson, & S. Spitzer (Eds.) Proceedings of the forty-third annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1494–1499). Philadelphia, PA. http://www.pmena.org/pmenaproceedings/PMENA%2043%202021%20Proceedings.pdf
Kim, M. Y., & Wilkinson, I. A. (2019). What is dialogic teaching? Constructing, deconstructing, and reconstructing a pedagogy of classroom talk. Learning, Culture and Social Interaction, 21, 70–86. https://doi.org/10.1016/j.lcsi.2019.02.003
Kitchen, J. (2005). Looking backward, moving forward: Understanding my narrative as a teacher educator. Studying Teacher Education: A Journal of Self-Study of Teacher Education Practices, 1(1), 17–30. https://doi.org/10.1080/17425960500039835
Krainer, K., Even, R., Rogers, M. P., & Berry, A. (2021). Research on learners and teachers of mathematics and science: Forerunners to a focus on teacher educator professional growth. International Journal of Science and Mathematics Education, 19(S1), 1–19. https://doi.org/10.1007/s10763-021-10189-8
LaBoskey, V. K. (2004). The methodology of self-study and its theoretical underpinnings. In J. Loughran, M. L. Hamilton, V. K. LaBoskey, & T. Russell (Eds.), International handbook of self-study of teaching and teacher education practices (pp. 817–869). Springer. https://doi.org/10.1007/978-1-4020-6545-3_21
Lischka, A. E., Hillman, S., & Kastberg, S. E. (2021). Seeking Understanding of Sustaining Discussions in Mathematics Methods through Self-Study of Teacher Education Practices. [Paper presentation]. American Educational Research Association Annual Conference. Online.
Loughran, J. (2006). Developing a pedagogy of teacher education: Understanding teaching and learning about teaching. Taylor & Francis. https://doi.org/10.4324/9780203019672-8
Loughran, J. (2014). Professionally developing as a teacher educator. Journal of Teacher Education, 65(4), 271–283. https://doi.org/10.1177/0022487114533386
Mewborn, D. S. (1999). Reflective thinking among preservice elementary mathematics teachers. Journal for Research in Mathematics Education, 30(3), 316–341. https://doi.org/10.2307/749838
Mewborn, D. S., & Tyminski, A. M. (2006). Lortie's apprenticeship of observation revisited. For the Learning of Mathematics, 26(3), 23–32. https://flm-journal.org/Articles/79737B7EDE7A641EB5A27DAE448B65.pdf
Munby, H., & Russell, T. (1994). The authority of experience in learning to teach: Messages from a physics methods class. Journal of Teacher Education, 45(2), 86–95. https://doi.org/10.1177/0022487194045002002
Pinnegar, S., & Hamilton, M. L. (2009). Self-study of practice as a genre of qualitative research: Theory, methodology, and practice (Vol. 8). Springer Science & Business Media. https://doi.org/10.1007/978-1-4020-9512-2
Reynolds, T. (2016). Striving for discussion: An analysis of a teacher educator’s comments in whole-class conversation. Studying Teacher Education: A Journal of Self-Study of Teacher Education Practices, 12(2), 205–221. https://doi.org/10.1080/17425964.2016.1192035
Saldana, J. (2016). The coding manual for qualitative researchers (3rd edition). Sage Publications.
Schuck, S., & Brandenburg, R. (2020). Self-study in mathematics teacher education. In J. Kitchen, A. Berry, S. M. Bulloch, A. M. Crowe, M. Taylor, H. Guðjónsdóttir, & L. Thomas (Eds.) International Handbook of Self-Study of Teaching and Teacher Education Practices (pp. 869–897). Springer. https://doi.org/10.1007/978-981-13-6880-6_29
Schuck, S., & Russell, T. (2005). Self-study, critical friendship, and the complexities of teacher education. Studying Teacher Education: A Journal of Self-Study of Teacher Education Practices, 1(2), 107–121. https://doi.org/10.1080/17425960500288291
Smit, J., AA van Eerde, H., & Bakker, A. (2013). A conceptualisation of whole‐class scaffolding. British Educational Research Journal, 39(5), 817–834. https://doi.org/10.1002/berj.3007
Smith, M. S., & Stein, M. K. (2011). 5 practices for orchestrating productive mathematics discussions. National Council of Teachers of Mathematics. https://doi.org/10.2505/9780873537452
Steele, M. D. (2005). Comparing knowledge bases and reasoning structures in discussions of mathematics and pedagogy. Journal of Mathematics Teacher Education, 8(4), 291–328. https://doi.org/10.1007/s10857-005-0854-4
Steffe, L. P., & D'Ambrosio, B. S. (1995). Toward a working model of constructivist teaching: A reaction to Simon. Journal for Research in Mathematics Education, 26(2), 146–159. https://doi.org/10.5951/jresematheduc.26.2.0146
Towers, J., Hall, J., Rapke, T., Martin, L. C., & Andrews, H. (2017). Autobiographical accounts of students’ experiences learning mathematics: A review. Canadian Journal of Science, Mathematics and Technology Education, 17(3), 152–164. https://doi.org/10.1080/14926156.2016.1241453
Vanassche, E. & Berry, A. (2020). Teacher educator knowledge, practice, and S-STTEP research. In J. Kitchen, A. Berry, S. M. Bulloch, A. M. Crowe, M. Taylor, H. Guðjónsdóttir, & L. Thomas (Eds.) International Handbook of Self-Study of Teaching and Teacher Education Practices (pp. 177–213). Springer. https://doi.org/10.1007/978-981-13-6880-6_6
Visnovska, J., & Cobb, P. (2015). Learning about whole-class scaffolding from a teacher professional development study. ZDM, 47(7), 1133–1145. https://doi.org/10.1007/s11858-015-0739-7
Walshaw, M., & Anthony, G. (2008). The teacher’s role in classroom discourse: A review of recent research into mathematics classrooms. Review of Educational Research, 78(3), 516–551. https://doi.org/10.3102/0034654308320292
Whitehead, J. (1989). Creating a living educational theory from questions of the kind, ‘How do I improve my practice?’ Cambridge Journal of Education, 19(1), 41–52. https://doi.org/10.1080/0305764890190106
Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27(4), 458–477. https://doi.org/10.5951/jresematheduc.27.4.0458